저는 로또는 재미 삼아서 가끔 하고 있는데 10여 년 전에는 계산에 의해서(확률과 통계) 맞춰볼 수 있다고 생각했었습니다. 그래서 한두 달간 푹 빠져 지냈던 거 같아요. 결론부터 말하자면, 불가능에 가까웠습니다. 이유는 확률이 너무 빈약하니까요. 그런데 희한하게 숫자 2개는 거의 맞추길래, 무조건 꼭 당첨번호 안에 드는 패턴이 있다고 믿었었답니다.
로또 1등에 당첨될 확률을 구하는 식을 세워 보면,
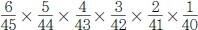
이렇게 세워볼 수 있고, 이 식을 계산하면 로또 1등에 당첨될 확률은 814만 5,060분의 1이 된답니다.
그런데 로또 당첨번호 알려준다고 광고하는 업자들 엄청 많죠? 그런거 하지 마세요. 상식적으로 그럼 그 사람들이 매주 복권 사서 당첨되면 되잖아요.
"당첨 안된 로또 용지 버리지 마세요."
"로또 뒷면 QR코드 비밀"
다 광고 멘트입니다.
목차

과거로 미래 예측이 가능하다고 믿는 로또 구매자들
로또 예측 사업을 한마디로 표현하자면, 과거를 기반으로 미래를 예측하는 일이겠죠.
그리고 그게 가능하다고 사람들에게 믿게끔 만드는게 이 사업의 핵심일 겁니다. 우리는 수많은 통계의 세상에서 살고 있습니다. 미래는 점점 더 빅데이터의 중요성이 부각되고, 테슬라가 경쟁력이 있는 이유 단 한 가지를 꼽으라면 테슬라 운전자가 자신도 모르게 테슬라에게 보내주는 엄청난 양의 각종 데이터들 일 겁니다.
정말로 예측할 수 있나?
이 질문에 대답은 수학적으로 증명이 끝난 사실부터 정리해 나가면 될 것 같습니다.
1, 한국로또의 가짓수가 814만 5060가지라는 것은 확률로 증명된 사실. (참)
2. 로또는 누가 뭐래도 "독립시행" 베르누이 시행’(Bernoulli’s trials)이다. (참)
독립시행이란?
로또의 이벤트는 매번 확률이 초기화된다는 얘기입니다. 베르누이 시행에 따르면 이번주에 나온 1등 숫자가 다음 주에도 나올 확률이 전혀 나오지 않은 가짓수와 동일한 814만 5060분의 1 임은 불변의 법칙입니다.
3. 자연과학을 인간이 완전히 이해하지 못하지 않느냐? (퀘스천)
이 세 가지 중에 나머지 3번에 로또 구매자는 기대를 하고 있는 것이고. 수학이 가진 한계점을 비집고 들어가는 것입니다. 예를 들자면, 수학은 이미 존재하는 사건에 대해 그 현상을 분석하는 데는 유용하지만, 해당 현상이 왜 생겨났는지는 증명 못하는 경우가 많기에 바로 그 부분을 믿으려는 자에게는 어필이 될 수 있는 것 같습니다.



로또 예측 판매 사업자들이 주장하는 법칙의 이해
"해당 사이트에서는 로또 1등 당첨자 후기가 나오고 통장 증명도 합니다."
당연히 그럴 수 있죠. 그건 위에 말한 해당 현상이 왜 일어났는지 수학적으로 증명 가능합니다. 814만 5,060분의 1 은 로또 복권 한 장을 샀을 때 확률이지만, 해당 사이트에서 얼마나 많은 구매가 일어났을까요?
얼마나 많은 사람들이 그들에게 받은 소위 무작위(저는 그렇게 봅니다.) 숫자에 기대를 걸며 베팅했을까요?
2014년도에 유명한 통계학자 분께서 명언을 하신 게 있습니다.
기자가 물었습니다.
"로또 당첨 확률을 높이는 가장 좋은 방법이 있을까요?"
"그럼요! 많이 사면 됩니다."
위의 결과는 위와 같이 이해해야 맞습니다.
통계는 무서운 학문입니다. 사람들이 쉽게 믿을 수 있는 오묘한 근거를 만들고, 여론도 조작할 수 있고, 자연현상도 마치 그럴 수 있다고 눈을 가릴 수 있습니다.

질문을 드려볼게요.
독일의 통계학자 발터 크래머는 벌거벗은 각종 숫자와 데이터를 가지고 만들어진 통계가 어떻게 사람들을 현혹하는지 설명합니다.
한 마을에 10명의 농부가 있습니다. 이들 농부 중 1명은 기업농으로 소 100마리를 가지고 있고, 나머지 농부 9명은 한 마리도 갖고 있지 못합니다.
그렇다면 통계적으로 이 마을의 농부들은 평균 몇 마리의 소를 가지고 있는 걸까요?
통계에서 나타나는 최빈(最頻) 값은 ‘0’ 마리이고, 중간값도 ‘0’ 마리인데 산술평균(算術平均)으로는 10마리가 됩니다. 산술평균은 통계에서 흔히 악용되는 숫자입니다. 로또 당첨자가 100만 명 중에 한 명인데 평균적으로 당첨률이 높다고 이야기하는 것은 바로 이러한 산술평균에 현혹되고 있는 것입니다.
그러나 소가 한 마리도 없는 9명의 농부에게는 아무 의미가 없기 때문입니다.
이처럼 산술평균은 사건의 실체를 은폐하는 데 주로 악용되고 있습니다.
로또 예측을 위해 사용한다는 법칙들에 대한 단상

| 마르코프 체인 [ Markov chains ] 을 이용한 주장 | 소련의 수학자 마르코프(Andrei A. Markov, 1856- 1922)가 도입한 확률 과정의 일종으로, 각 시행의 결과가 바로 앞의 시행의 결과에만 영향을 받는 일련의 확률적 시행을 말한다. 마르코프 과정(Markov process)이라고도 한다. |
우리가 위에서 이미 인정했듯이 제 1법칙 로또는 독립 시행이다에 위반. 이 법칙은 로또에 쓰일 수가 없습니다. |
|
| 몬테카를로 분석 [ Monte Carlo analysis 을 이용한 주장 | 난수를 이용하여 확률 현상을 수치 실험적으로 관찰하는 방법. 이것이 널리 사용되기 시작한 것은 1946년에 노이만(von Neumann)과 울람(Ulam)이 핵반응 계산을 했을 때부터였는데, 오늘날에는 컴퓨터의 보급에 힘입어 공학이나 물리학과 더불어 특히 OR 분야에 널리 적용 되고 있다. |
몬테카를로라는 거창한 이름을 붙였지만, 몬테카를로는 오류를 뜻합니다. 1913년 8월 18일 모나코 몬테카를로의 호화로운 보자르 카지노에서 27번이나 검은색 구슬이 연속해서 떨어지는 진귀한 일이 벌어졌다. '이제는 붉은색 구슬이 나오겠지...' 라고 생각하며 계속 반대편에 베팅한 게이머들이 이러한 생각으로 거액을 잃었는데, 이 용어의 다른말은 "도박사의 오류" 입니다. 즉 오류를 법칙으로 둔갑시켰다고 생각하는게 합리적입니다. |
|
| 패턴을 이용하여 당첨번호에 접근한다는 주장 | ‘소수의 법칙’(Law of small numbers) |
패턴에 대한 생각은 각자가 다를 수 있습니다. 숫자 사이의 간격일 뿐인데 그 안에 확률이 있다고 믿을수도 있기 때문입니다. 통계학은 이 숫자들을 패턴화 한거니까 로또 당첨번호 예측의 가장 좋은 주장이기도 합니다. 그러나, 로또를 패턴화 하기 위해서는 자연과학을 다시 말해야 합니다. 우리가 알지 못하는 어떤 반응으로 인해서 자연 속에 존재하는 패턴을 찾아내는 것 입니다. 이 패턴 개념이 힘을 얻으려면 자연속에서 로또 구슬이 어떤 반응을 일으키는지 가설이 필요 할 겁니다. 소수의 법칙이란 작은 표본에서 등장한 패턴이 전체 표본에서도 같은 패턴으로 나온다고 믿는 걸 말한다. 학문적으로는 특정기간에 무작위로 수집된 소표본은 대표본에서 나오는 진실된 확률분포를 보여주지 못한다고 알려져 있습니다. 즉 일부 과거의 지표로 미래를 추정하는 소수의 법칙으로는 절대 로또숫자를 예측할 수 없다는 이야기 입니다. |
|
믿는 건 자유. 허나 나 같으면 그 돈으로 로또 한 장 더 사겠네
그러나, 오늘 저의 설명과 주장은 신을 믿느냐, 안 믿느냐와 크게 다르지 않을 것 같습니다.
보통 사람들은 믿고 싶은 것을 믿으며, 아무리 작은 확률이라도 가능성이 있다고 스스로 판단하는 것에 베팅을 하니, 구구절절한 이야기들은 거의 도움이 안 될 듯합니다.

그러나, 결론적으로 가장 좋은 이야기를 하나 남기고 오늘 포스팅 마치려고 합니다.
확실하지 않은 당첨 번호 받는데 몇만 원을 쓰느니, 그 돈만큼 로또 구매에 투자하는 게 훨씬!! 아주 확실하게 훨씬!! 당첨 확률을 높일 수 있는 가장 좋은 방법입니다.
'어떻게 생각해?' 카테고리의 다른 글
| 각종 양식 다운로드 무료 제공 (2) | 2023.09.13 |
|---|---|
| 백강현 서울과학고 자퇴 사건으로 보는 천재의 삶 (1) | 2023.08.24 |
| 크리스토퍼 놀란 감독의 색다른 영화 작품 BEST 3 (0) | 2023.08.16 |
| 소시오패스 테스트로 알아보는 소시오패스 특징 (0) | 2023.08.10 |
| 한국의 MZ 세대 vs 일본의 유토리 세대 , 사토리 세대 (0) | 2023.07.26 |




